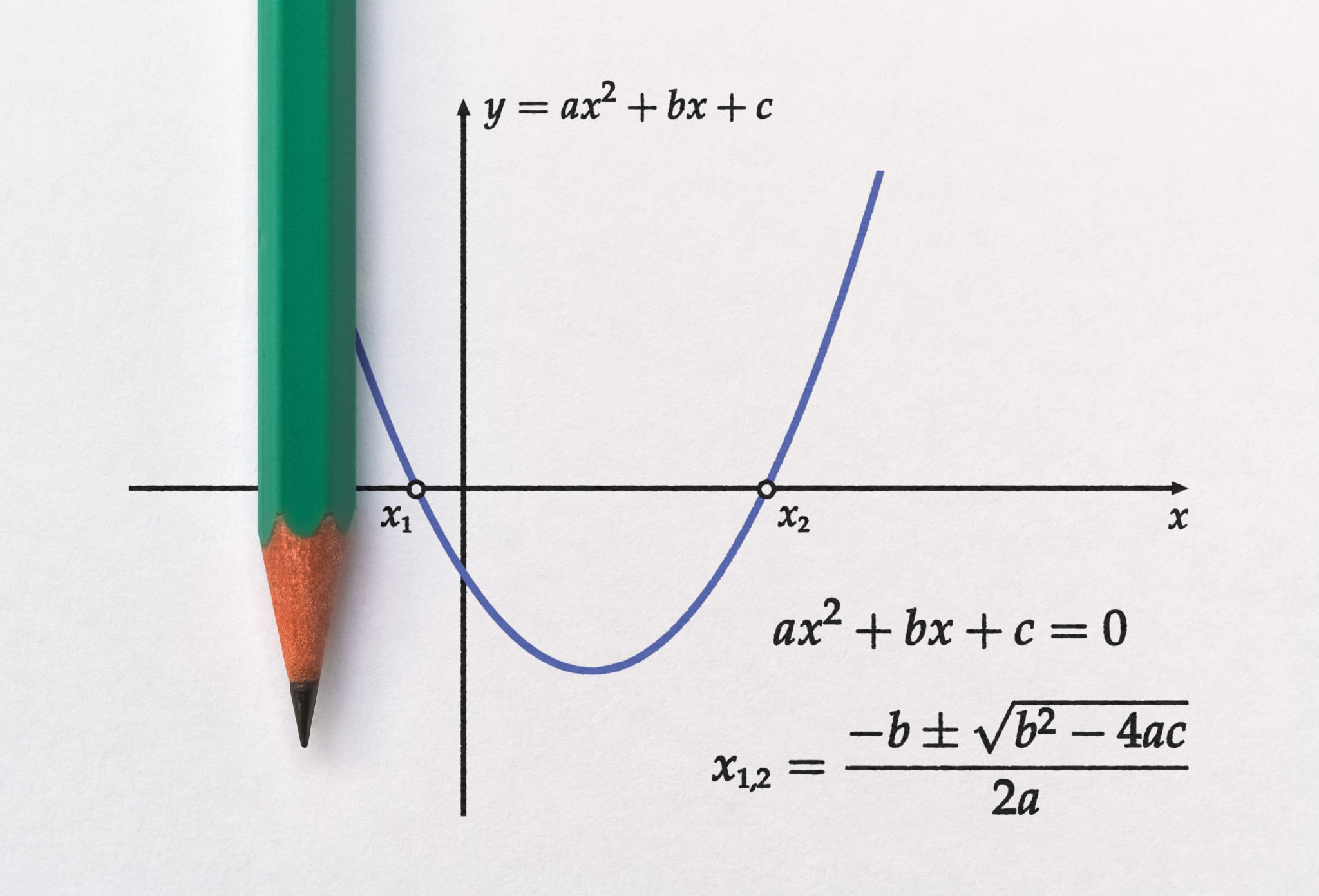Comprehensive Guide to Mastering Algebra: Tips and Tricks
Understanding Algebra: The Basics
Algebra might seem daunting at first, but it's a branch of mathematics that opens up a world of logic and reasoning. At its core, algebra is about finding the unknown or putting real-life variables into equations and then solving them. The key to mastering algebra is to understand its fundamental principles rather than memorizing formulas.

Essential Algebraic Concepts
Before diving into solving equations, familiarize yourself with essential concepts like variables, constants, coefficients, expressions, and equations. A variable represents an unknown number, while a constant is a fixed value. The coefficient is a number that multiplies the variable, and expressions are combinations of constants, variables, and operations. Equations are statements that two expressions are equal.
Understanding these concepts lays the groundwork for more advanced topics. Ensure you are comfortable with basic arithmetic operations as they are foundational to manipulating algebraic expressions.
Solving Linear Equations
Linear equations are the simplest form of algebraic equations. They represent a straight line when graphed and have no exponents higher than one. The general form of a linear equation is ax + b = c, where a, b, and c are constants. To solve these equations, isolate the variable on one side.

Step-by-Step Approach
Here’s a systematic approach to solving linear equations:
- Simplify both sides of the equation by combining like terms.
- Use addition or subtraction to move constants to one side of the equation.
- Use multiplication or division to solve for the variable.
Practice regularly with various problems to build confidence and improve your problem-solving skills.
Tackling Quadratic Equations
Quadratic equations are a bit more complex but manageable with practice. They take the form ax² + bx + c = 0. These equations can be solved using different methods such as factoring, completing the square, or the quadratic formula.
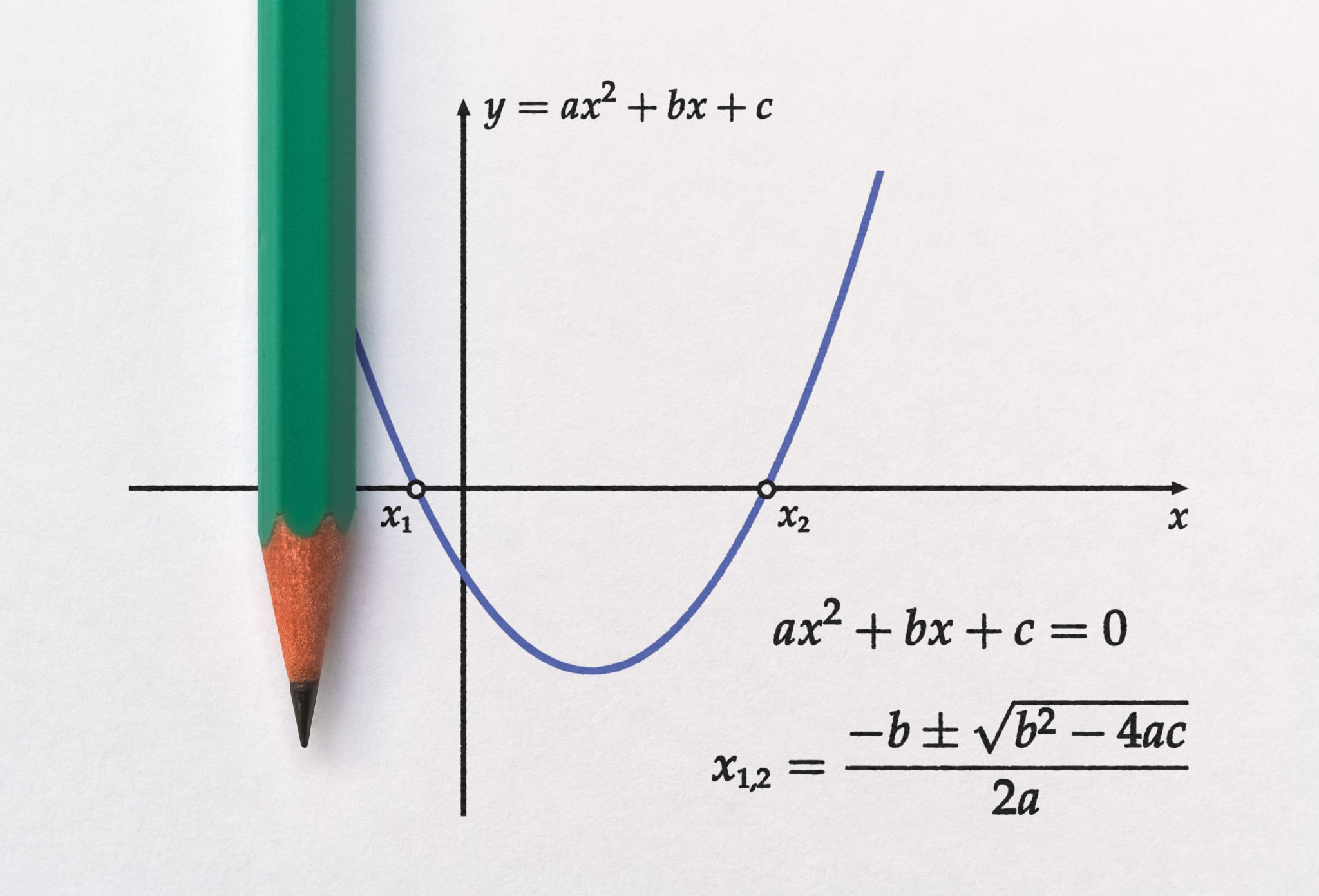
The Quadratic Formula
The quadratic formula is a powerful tool for solving any quadratic equation: x = (-b ± √(b² - 4ac)) / 2a. This formula will work in every scenario, even when factoring is difficult or impossible. Ensure you understand how to apply this formula correctly and practice using it in different problems.
Polynomials and Factoring
Polynomials are algebraic expressions that include two or more terms. Factoring is a critical skill in algebra that involves breaking down polynomials into simpler components. Mastering this skill simplifies solving complex equations.

Common Factoring Techniques
Here are some common techniques for factoring polynomials:
- Greatest Common Factor (GCF): Identify and factor out the highest common factor from all terms.
- Difference of Squares: Use the identity a² - b² = (a + b)(a - b).
- Trinomials: Factor quadratic trinomials into two binomials.
The Importance of Practice and Persistence
The ultimate key to mastering algebra lies in consistent practice. Working through problems regularly helps reinforce concepts and improve problem-solving speed and accuracy. Don’t be discouraged by mistakes; they are valuable learning opportunities.
Utilize resources such as textbooks, online tutorials, and study groups to broaden your understanding. Remember that persistence is crucial; over time, the principles of algebra will become second nature.